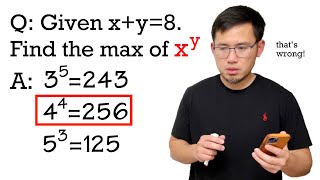How Cauchy would find the maximum of sqrt(x)+sqrt(y)

Given x+2y=4, we want to find the maximum of sqrt(x)+sqrt(y). We can do this the Calculus 1 way (finding the critical number from the first derivative, then testing out if it's a min or max), but we can also use the Cauchy-Schwarz inequality. The version we will use is (a^2+b^2)(c^2+d^2) is greater than or equal to (ac+bd)^2. To read more, you can see
https://en.wikipedia.org/wiki/Cauchy%E2%80%93Schwarz_inequality Cauchy-Schwarz inequality is a big topic for high school students in Taiwan. It's definitely not easy sometimes but it is very cool.

The derivative way: Calculus 1: Given x+2y=4, find the max of sqrt(x)+sqrt(y)
https://youtu.be/utXCYoD37-M

Here's a video that I did with Mr. Li when I was in Taiwan. Finding the maximum of 2/sin(theta)+3/cos(theta) for theta from 0 to pi/2 (這是我跟李翰老師 @lihanmath 合作影片之一. 這應該是台灣史上最有名的大學數學聯考題) https://youtu.be/USQmVs-874g?si=7Yj9HpdXBzDzJy8r
----------------------------------------
Big thanks to my Patrons for the full-marathon support!
Ben D, Grant S, Mark M, Phillippe S. Michael Z, Camille E.
Nolan C. Jan P. Devun C. Stefan C. Ethan BW
Didion S. NN Minkyu Y Brandon F

💪 Support this channel and get my math notes by becoming a patron: https://www.patreon.com/blackpenredpen
🛍 Shop my math t-shirt & hoodies: https://amzn.to/3qBeuw6
----------------------------------------
#blackpenredpen #math #calculus #apcalculus