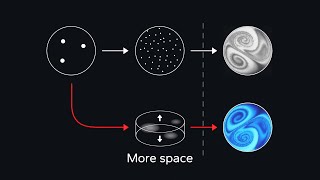
How do you simulate what isn‘t there – and still make sense of it?

This is the second part in a series about Computational Fluid Dynamics where we build a Fluid Simulator from scratch. We derive the Macroscopic Perspective (Continuum) from the Microscopic Perspective (Molecules) covering: Collective Molecular Behavior, Local (Non-)Equilibria, Classical Statistical Mechanics, Rarefied Gas Dynamics, and Continuum Gas Dynamics. The Macroscopic Perspective provides the ground for the next part where we make it all numerically accessible - the Discretization. Timetable: ----------------- 00:00 - Why we need a Macroscopic Perspective 01:44 - Particles Collective Behavior 05:33 - Using Equilibria for Reduction 08:17 - Statistical Mechanics and Rarefied Gas Dynamics 12:00 - Continuum Gas Dynamics 16:09 - Building Macroscopic Quantities 23:05 - Linking Macroscopic Quantities 34:09 - Recap Selected Papers and Learning Resources: ------------------------------------------------------------------- Sorted by Topics: 01:44 - Local (Non-)Equilibrium; Necessity of Collisions; Fluctuations; Molecular Chaos; Initial Perturbation; Statistical Perspective; Statistical Ensemble Averaging; Time Reversibility (to be discussed), Equilibria of different Degrees-of-Freedom (to be discussed): [1,2,3] 08:17 - Rarefied Gas Dynamics: [1,4] 08:17 - Phase Space (one-particle vs. N-particle): [1,5,6] 08:17 - Boltzmann Equation derived via BBGKY Hierarchy from Liouville Theorem: [6] 12:00 - Continuum Gas Dynamics, Continuum Hypothesis/Assumption, Alternative Flow Regimes Classifications: [1] 12:00 - Local Knudsen Number and alternative Rarefaction Indicators: [1,4] 16:09 - Macroscopic Quantities: Density, Flow Velocity, Pressure, Temperature [1] 23:05 - Macroscopic Equations: Conservation Laws; Mass; Momentum; Energy [1] 27:20 - Navier-Stokes Equations; Densities of Forces; Pressure Gradient; Viscosity: [1,7] 27:41 - Time Derivatives along with flow; Lagrangian vs. Eulerian Formulation; Lagrangian vs. Eulerian Coordinate Systems: [8] 30:12 - Velocity and Temperature Profiles for Couette Flow: [9] 32:45 - Macroscopic Equations: Equations of State; Ideal Gas Law; Calorically Perfect Gas: [1] Selected References: [1] - Lecture Notes: from "http://volkov.eng.ua.edu/ME591_491_NEGD/2017-Spring-NEGD-01-ElemKineticTheory.pdf" to "NEGD-06" [2] - Paper: Maes, Christian, and Karel Netočný. "Time-reversal and entropy." Journal of statistical physics 110.1 (2003): 269-310. [3] - Paper: "Parker, J. G. Rotational and vibrational relaxation in diatomic gases. The Physics of Fluids 2.4 (1959): 449-462." [4] - Paper: Macrossan, M. N. "Scaling parameters for hypersonic flow: correlation of sphere drag data.", 2007. [5] - Lecture Notes: "Cerfon, Antoine. Mechanics (Classical and Quantum). https://www.math.nyu.edu/~cerfon/mechanics.html" [6] - Lecture Notes: "Kenkre, V. M.. Statistical Mechanics. https://www.unm.edu/~aierides/505/" specifically ".../bbgky2.pdf" & ".../bbgky3.pdf" [7] - Book: Anderson, John D. "Governing equations of fluid dynamics." Computational fluid dynamics. Springer, Berlin, Heidelberg, 1992. 15-51. [8] - Essay: Price, James F. "Lagrangian and eulerian representations of fluid flow: Kinematics and the equations of motion." MIT OpenCourseWare, 2006. [9] - Paper: Marques Jr, W., G. M. Kremer, and F. M. Sharipov. "Couette flow with slip and jump boundary conditions." Continuum Mechanics and Thermodynamics 12.6 (2000): 379-386. Disclaimer: ------------------ This series focuses specifically on the aspect of information reduction in dynamical systems. For the sake of clarity, I had to omit many interesting aspects of the topics addressed in the video. So, the video itself is a reduction. :-) Please note: ------------------ Watching this video with very low resolution produces the continua right away :-), thanks to the video compression! I hope you enjoyed this little braintruffle! If you like this series and want to support my work, you may consider subscribing to the channel. I would really appreciate it! Thank you for watching and I hope to see you next time!