Linear Algebra Example Problems - Vector Space Basis Example #2

http://adampanagos.org

Course website: https://www.adampanagos.org/ala

In this video we determine if a set of given vectors is a basis for R3.

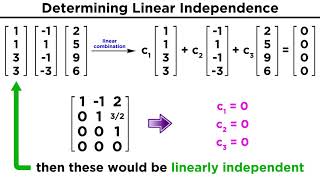
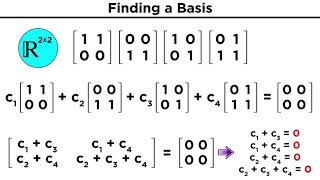
We know that in general, a basis for Rn requires n linearly independent vectors. Since we're working with R3 in this problem, we require 3 linearly independent vectors to form a basis for R3.

Two different methods are used to check for linear independence of the vectors. In the first, we construct a matrix and perform row operations to show that we do NOT obtain a pivot in each column. This implies that there is a free variable in the system and thus many non-trivial solutions to Ax = 0. Thus, the vectors are NOT independent.

In the second method we compute the determinant of the matrix. Since the determinant is equal to zero, we can conclude once again that the vectors are NOT independent.

Since we've shown that the three vectors are not linearly independent, then they do not form a basis for R3.

If you enjoyed my videos please "Like", "Subscribe", and visit http://adampanagos.org to setup your member account to get access to downloadable slides, Matlab code, an exam archive with solutions, and exclusive members-only videos. Thanks for watching!