Metric Spaces Introduction, Real Analysis II

In this lecture, I define the concept of a metric space, a fundamental domain in real analysis. A metric space requires two things: a set M and a function D that measures the distance between elements in M. We'll explore the four essential properties a metric must satisfy: positivity, non-degeneracy, symmetry, and the triangle inequality.

(MA 426 Real Analysis II, Lecture 4)

We begin by defining these properties in detail. Positivity means the distance is never negative. Non-degeneracy ensures the distance is zero if and only if the elements are the same. Symmetry indicates that the distance from X to Y is the same as from Y to X. The triangle inequality states that the direct distance between two points is always less than or equal to the distance traveled via a third point.

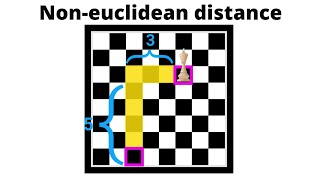
To illustrate, we explore a discrete metric space, where the distance as either 0 or 1. We'll verify this space meets all metric properties. Next, we examine the taxi cab metric on the xy-plane, calculating distances based on city block paths rather than straight lines. We'll check that this metric also satisfies the four properties and discuss its unique geometric implications, such as diamond-shaped circles.

Finally, I demonstrate that any normed vector space induces a metric, proving that the norm's properties ensure the metric properties. This concludes with a discussion on the broader implications and limitations of metrics derived from norms.

#advancedcalculus #MathLecture #MetricSpace #RealAnalysis #Mathematics #MathProof #DiscreteMetric #TaxiCabMetric #EuclideanSpace #Geometry #NormedVectorSpace #MathConcepts