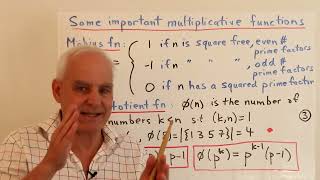Multiplicative functions and Dirichlet Series via Boxes II| Math Foundations 243 | N J Wildberger

We introduce Dirichlet series, which are particular series coming from number theory, generalizing the Riemann zeta function, in a somewhat novel way using box arithmetic. Let's try to avoid nonsensical appeals to "doing an infinite number of things", and instead give a precise arithmetic with always well-defined objects. The natural operations of Box Arithmetic start with addition, then multiplication and then the caret operation, which we could call "caretation".

By combining addition and caretation, we get an algebraic structure which effectively encodes the usual Dirichlet series. But we are able to think about the associated algebra in quite an interesting alternative way, including insights into novel notation.

Video Contents:
00:00 Introduction
3:39 Box Notation
6:50 Algebra With Poly*
10:10 The Plus/Caret Algebra of Poly*
15:02 (mlist ) Of a Poly*
17:18 Caret Convulsion Of mlist
22:42 The Multiplicity list
27:23 An Alternative

***********************
My research papers can be found at my Research Gate page, at https://www.researchgate.net/profile/Norman_Wildberger

My blog is at http://njwildberger.com/, where I will discuss lots of foundational issues, along with other things.

Online courses are being developed at openlearning.com. The first one, already underway, is Algebraic Calculus One at https://www.openlearning.com/courses/algebraic-calculus-one/ Please join us for an exciting new approach to one of mathematics' most important subjects!

If you would like to support these new initiatives for mathematics education and research, please consider becoming a Patron of this Channel at Patreon, https://www.patreon.com/njwildberger Your support would be much appreciated.