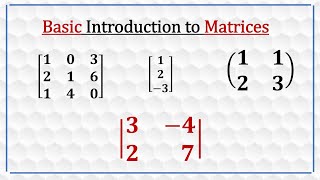
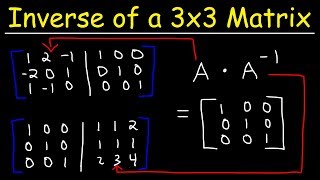
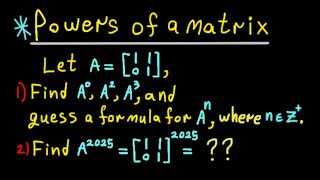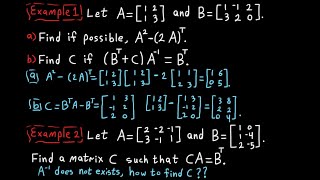Negative powers of a matrix

❖ In the video, we learn about the negative powers of a matrix.

❖ The tutorial starts by calculating A^(-1), A^(-2), and A^(-3), then moves on to formulating a general formula for A^n where n is any negative integer. By using this formula, we compute A^(-2025)

❖ The negative power A^n of a matrix A, where n is a negative integer is defined as the matrix product of n copies of the inverse of A

To find the negative power of A,
the inverse of A has to be exist.
(so, A^(-1) has to be exist).

To find A^(-1),
A must be a square matrix.
This means that
the number of rows = the number of columns
(for example, its dimensions could be 2x2, 3x3, etc.).

A^0 is defined to be
A^0=I_n
where I_n is an identity matrix with the same size as A.

❖ The number of rows and columns that a matrix has is called its size, its order, or its dimension.

0:00 ❖ Introduction
1:02 The condition and properties
6:24 Review from the previous video
9:45 Solve 3
18:15 Solve 4
19:01 Final formula of A

The link to this playlist (Linear Algebra):
https://www.youtube.com/playlist?list=PLPm9fyDNbwj9zUIHKYfNwkfeWWBamk-q_

My Website:
https://www.Mulkek.com

Subscribe to My Channel to check out more videos:
https://youtube.com/c/Mulkek