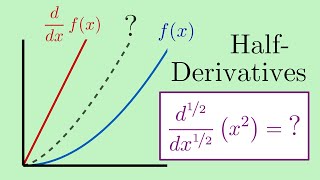
Secret Kinks of Elementary Functions

What happens to graphs between degrees of polynomials? How can we draw complex inputs and outputs in 2 dimensions? And what will we see if we try?

00:00 Intro
01:14 The Messy Powers
04:41 About Complex Numbers
07:15 Importing a Function into the Complex Plane
12:19 Overshooting with Euler
17:27 Roots
23:30 Flower Pressing
25:47 Down to and Around Zero
27:06 The Big Bang
29:34 Enjoy!
30:53 Bonus Functions

Correction: 03:26 The first x in the expansion is raised to 1.4. It should be raised to 1.6.

DESMOS GRAPHS:
===============
5th degree polynomial
https://www.desmos.com/calculator/e9ti5bi2lr

x^p
https://www.desmos.com/calculator/eob3uhfplp

x^x
https://www.desmos.com/calculator/um2wwsev11

base Gaussian
https://www.desmos.com/calculator/sl4ucvcaca


More on Complex Numbers:
https://youtu.be/nlqOQ0vJF0Q


Music by:
@timkuligfreemusic (intro)
@Lisayamusic (the rest of the video)

Notes:
At 2:46, when we start converting fractional powers, the fractions must be reduced to lowest terms before we use them to assign the degree of root and power under it.