Solving a Cubic Equation Using a Triangle

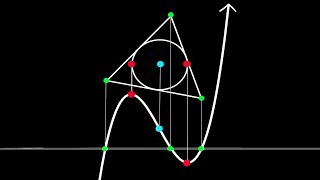
There is this surprising fact about cubic equations with 3 real solutions where an equilateral triangle centered on the inflection point can always be scaled/rotated by some amount such that its vertices will line up with the roots of the equation.

But is there any way that this can be used to solve a cubic of this form? Of course there is, just some ingenious work with trigonometry gets us to the answer, and that is what is outlined in this video along with example(s).

With something as complicated to solve as a cubic equation, an elegant geometric solution is very beautiful to see.

Timecodes:
0:00 - Intro and statement
3:04 - Analysis and formulation
11:25 - Representation in a cubic equation
14:53 - Worked example
20:16 - Intuition and connections to the cubic formula

Sources and other tidbits:
Info about cubic functions and their properties: https://en.wikipedia.org/wiki/Cubic_function
The rise of the triangle (and incircle pertaining to the extrema) from a Joukowsky map: https://maa.tandfonline.com/doi/full/10.1080/00029890.2019.1528814#.YRBwTi295B1
Visualization in Desmos: https://www.desmos.com/calculator/890doczgw7
A geometric quartic construction: https://imgbb.com/LSHdq3B

Twitter - https://twitter.com/michaelmaths_
Instagram - https://www.instagram.com/michaelmaths_

#SoME1 #3b1b