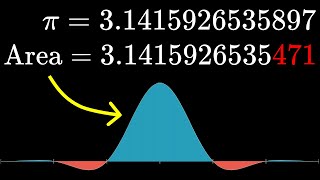
The Verhoeff-Gumm Check Digit Algorithm #SoME3

Rediscover and explore the Verhoeff-Gumm algorithm, a check digit formula which is more resilient to common errors than the Luhn algorithm, which is widely used in credit card numbers, IMEI numbers and more.

Historical Notes:
"Error Detecting Decimal Codes" [1], a PhD thesis by J Verhoeff was published in 1969. It showed how the vast majority of digit typos were single digit or transposition errors, traditional "modulo 10" algorithms always missed some transposition errors, and introduced a novel class of algorithms based on "the dihedral group of order 10" (pentagon flips and rotations). In section 4.4, Verhoeff outlines using "search program" to find a permutation function that is optimal for detecting errors. A formal proof of the permutation's correctness is omitted. I found Verhoeff's writing to be difficult to approach, so I recommend a section in "Contemporary Abstract Algebra" (seventh edition) by Joseph A Gallian (pg 111-114) for a clearer write-up. A witty quote from Verhoeff in the introduction made me chuckle: "[I believe] that the codes explained in chapter 4 provide the first practical application of the dihedral group. This would illustrate the old saying that all beautiful mathematics will find an application, sooner or later."

In 1985, H. Peter Gumm published "A new class of check-digit methods for arbitrary number systems" [2]. It starts with a dense proof that "modulo 10" (indeed modulo 2k) formulas will always be flawed. The paper then justifies the use of the dihedral group, which to me sounded like a mathematician walking around a store looking for the right outfit ("needs cancellation", "should be associative", "finite members", "can generalize for any even number"). Gumm then *proves* an algorithm using D_s works, using the number pair notation and a permutation function tau.

Gumm claims to have been unaware of Verhoeff's work. Additionally, Gumm adds a proof and a way to scale it beyond 10 digits, so I decided to credit them both with discovering the algorithm in this video.

A variant of the algorithm saw use (an may still see use) on German Banknotes [4].

Felix Klein (same as the Klein bottle) was an important contributor to group theory [3], and was chosen to be the cardholder in the intro. Likewise, Évariste Galois coined the term "group" and was thus chosen to be the online vendor.

[1] https://ir.cwi.nl/pub/13046/13046D.pdf
[2] https://www.researchgate.net/publication/3084126_A_new_class_of_check-digit_methods_for_arbitrary_number_systems_Corresp
[3] https://archive.org/details/vergleichendebe00kleigoog/page/n20/mode/2up
[4] http://ocs.ef.jcu.cz/index.php/inproforum/INP2016/paper/viewFile/794/565

Expanding the Mathematical Toolbox:
A key concept in Group Theory is the idea of sets, which is covered very well in [4]. Groups are introduced well in [5] and I hope the author continues the series.
The Rubix cube can be analyzed using group theory [6] or with "graphs" [7], which are both useful when dealing with so many possible states.

[4] https://youtu.be/dKtsjQtigag "What IS a Number? As Explained by a Mathematician" by Another Roof
[5] https://youtu.be/KufsL2VgELo "Researchers Use Group Theory to Speed Up Algorithms — Introduction to Groups" by Nemean
[6] https://youtu.be/FW2Hvs5WaRY "Group theory 101: How to play a Rubik’s Cube like a piano - Michael Staff" by TED-Ed
[7] https://youtu.be/wL3uWO-KLUE "The algorithmic trick that solves Rubik’s Cubes and breaks ciphers" by polylog

Animations were made by Kaylee L with Manim Community edition (https://www.manim.community/) taking about 7k lines of Python code to make. Narration by James K.

Sound effects from YouTube Audio Library
- Battle Crowd Celebrate Stutter
- Punchline Drum

This was an entry into Summer of Math Exposition 3 #SoME3
- https://some.3b1b.co/

0:00 Luhn Algorithm (and its flaw)
1:39 How could we fix the flaw?
2:21 Basic Integer Operations (how they don't help)
3:12 Rotating and Flipping Shapes is order dependent
4:16 Combining Pentagons (function composition)
5:30 "Packing the box" with pentagons (associativity/inverses)
6:56 Do our pentagons work for all transpositions? (Cayley Table)
8:29 Adding a preprocessing step (sigma function)
9:30 How to prove if sigma works (converting to integer pairs)
11:56 Proving Gumm's sigma function does work
13:12 Expanding sigma into digit permutation
13:38 Scaling up to 3 or more digits/pentagons
15:06 Summarizing the Verhoeff-Gumm Algorithm (and the variants)
16:00 Group theory is all about surprising symmetries